Kurs maturalny z języka angielskiego!
kurs-maturalny-jezyk-angielski
PROGRAMOWANIE I ALGORYTMY
- Kurs języka Python
- Wstęp do Python
- Python — instrukcja warunkowa
- Python — pętle
- Python — napisy
- Python — listy — tablice jednowymiarowe
- Python — listy — tablice dwuwymiarowe
- Python — funkcje
- Python — krotki
- Python — słowniki
- Python — obsługa plików
- Python — rekurencja
- Moduły
- Algorytmy w Pythonie
- Z dziesiętnego na dowolny system liczbowy w Python
- Pierwiastki funkcji kwadratowej w Pythonie
- Suma cyfr w Pythonie
- Liczby doskonałe w Pythonie
- Pierwiastkowanie w Pythonie
- Ciąg Fibonacciego w Pythonie
- Czy pierwsza w Pythonie
- Faktoryzacja liczby w Pythonie
- Sito Eratostenesa w Pythonie
- Algorytm Euklidesa — Python
- Schemat Hornera w Python
- Potęgowanie szybkie w Pythonie
- Programowanie zachłanne, wydawanie reszty
- Czy palindrom w Pythonie
- Czy anagramy w Pythonie
- Szyfr Cezara w Python
- Wyszukiwanie wzorca w tekście — python
- Wyszukiwanie binarne w Pythonie
- Sortowanie bąbelkowe w Pythonie
- Sortowanie przez selekcję w Pythonie
- Sortowanie przez wstawianie w Pythonie
- Sortowanie przez scalanie w Pythonie
- Sortowanie szybkie w Pythonie
- Sortowanie kubełkowe w Pythonie
- Odwrotna Notacja Polska w Pythonie
- Bisekcja w Pythonie
- Z dziesiętnego na dowolny system liczbowy w Python
- Przydatne funkcje w Pythonie
- Zbiór zadań
- Suma dwóch liczb
- Zamiana wartości zmiennych
- Litery w przedziale
- Godziny i minuty
- Liczby w jednym wierszu
- Czy jesteś pełnoletni?
- Ciepło, zimno, gorąco
- Cyfra na tekst
- Maksymalna z trzech liczb
- Miejsca zerowe funkcji kwadratowej
- Suma n liczb
- Gwiazdkowy prostokąt
- Trzy razy dwa
- Liczby naprzemiennie
- Kolejne potęgi liczby 2
- Zamiana na duże
- Tyle samo zer i jedynek
- Zlicz wystąpienia słowa "oko".
- Zliczanie wystąpień liter
- Najdłuższy ciąg tych samych liter
- Dziedziczenie, pojazdy
- Dziedziczenie, osoby
- Suma dwóch liczb
- Kurs maturalny z informatyki
- Matura z informatyki
- Systemy liczbowe
- Struktury danych
- Arkusze maturalne
- Algorytmy maturalne
- Badanie czy liczba jest pierwsza
- Wyszukiwanie binarne
- Palindrom
- Wysz. wzorca w tekście
- Schemat Hornera
- Porządkowanie zbiorów
- Sortowanie bąbelkowe
- Sortowanie przez selekcję
- Sortowanie przez wstawianie
- Sortowanie przez scalanie
- Sortowanie kubełkowe
- Sortowanie szybkie
- Szyfrowanie
- Szyfr przestawieniowy
- Szyfr cezara
- Operacje na ułamkach
- NWW
- Przeszukiwanie z wartownikiem
- Lider w zbiorze
- Jednoczesne wysz. min. i max.
- Potęgowanie szybkie
- Połowienie przedziałów
- Metoda trapezów
- Metoda prostokątów
- Newton-Raphson
- Anagramy
- Liczby doskonałe
- Nierówność trójkąta
- Dwa odcinki
- Odwrotna notacja polska
- Rozkład liczby na czynniki
- Sito Eratostenesa
- Pozycyjne reprezentacje liczb
- Ciąg Fibonacciego
- Wyszukiwanie elementu min/max
- Elemement min. i maks.
- Algorytm Euklidesa
- Zadania - poziom podstawowy
- Zadania - poziom rozszerzony
- FRAKTAL
- Nagrody
- Edycja I
- Zadania z I Edycji
- Omówienie zadań I rundy
- Edycja II
- Zadania z II edycji
- Omówienie zadań z II edycji
- Edycja III
- Zadania z III edycji
- Omówienie zadań z III edycji
- Edycja IV
- Zadania z IV edycji
- Omówienie zadań IV rundy
- Edycja V
- Zadania z V edycji
- Edycja VI
- Zadania z VI edycji
- Edycja VII
- Zadania z VII edycji
- Edycja VIII
- Zadania z VIII edycji
- Omówienie zadań z VIII edycji
- Nagrody
- Rozwiązania zadań maturalnych
Zajęcia maturalne z informatyki
Olimpiada Informatyczna Juniorów
-
Prowadzący: Marcin Kasprowicz
- właściciel serwisu algorytm.edu.pl
- wrzesień 2024 — start zajęć
- czytaj więcej
Drzewo BST z historią (zbiory z historią)
Gdy potrzebujemy zapamiętać poprzednie wersje drzewa BST możemy tworzyć kolejne jego kopie. Niestety takie rozwiązanie posiada bardzo poważną wadę. Złożoność czasowa i pamięciowa programu znacznie się pogarsza. Rozwiązaniem tego problemu może być tworzenie kopii tylko tej gałęzi, po której aktualnie się poruszamy dodając klucz. Rozpatrzmy następujący ciąg liczb:
$$4,\ 7,\ 3,\ 8\ 1,\ 6,\ 10$$
Drzewo BST będzie wyglądać jak na rysunku poniżej:
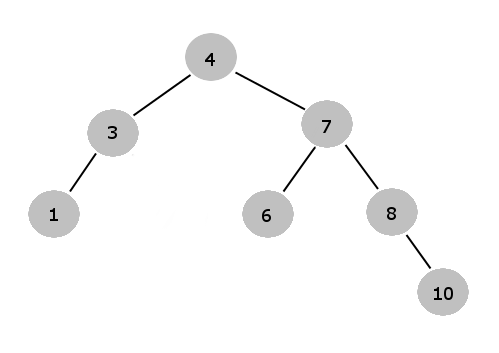
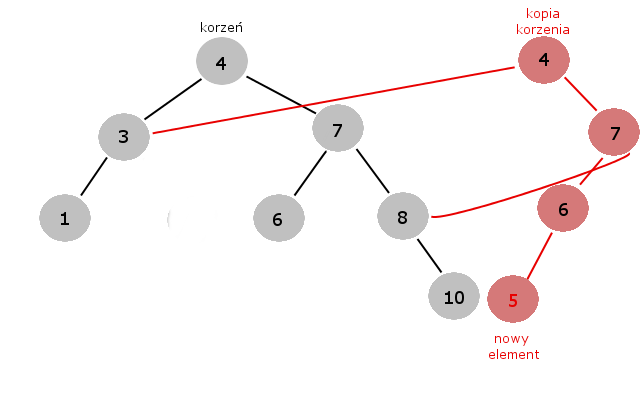
Teraz chcemy dodać następny element jednocześnie pamiętając poprzednią wersję drzewa. Tworzymy kopię korzenia (na przykład dodając ją jako kolejny element wektora), następnie tworzymy tylko te elementy drzewa, przez które będziemy przechodzić, a ci synowie, którzy nie będą odwiedzeni pozostają pozostają bez zmian, przypisując do nich odpowiedni wskaźnik ojca.
Załóżmy, że chcemy dodać do naszego drzewa liczbę 5. Poniższy rysunek przedstawia zaistniałą sytuację.