Rekurencja w C++

Rekurencja zwana rekursją, polega na wywołaniu przez funkcję samej siebie. Algorytmy rekurencyjne zastępują w pewnym sensie iteracje. Niekiedy problemy rozwiązywane tą techniką będą nieznacznie wolniejsze (wiąże się to z wywoływaniem funkcji), natomiast rozwiązanie niektórych problemów jest dużo prostrze w implementacji.

Przykład 1

Prześledźmy program wyznaczający sumę n kolejnych liczb naturalnych.

#include <iostream>
using namespace std;

long long suma(int n)
{
	if(n<1) 
		return 0;
	
	return n+suma(n-1);
}

int main()
{
	int n;
	
	cout<<"Podaj liczbę: ";
	cin>>n;
	
	cout<<"Suma "<<n<<" kolejnych liczb naturalnych wynosi "
<<suma(n)<<endl;

	return 0;
}

Załóżmy, że na wejściu podaliśmy liczbę 5 (program ma wyznaczyć sumę 1+ 2+ 3 + 4 + 5).

wynik = suma(5);

Funkcja suma(n), wywołała się z argumentem równym 5. Najpierw sprawdzamy, czy n< 1 (5 < 1). Warunek jest fałszywy, przechodzimy więc do następnej linijki return 5 + suma(5 - 1) . Funkcja suma wywołana została przez samą siebie z argumentem równym 4, a więc mamy:

wynik = suma(5) = 5 + suma(4),

daną czynność powtarzamy do momentu, gdy argument osiągnie wartość 0, wtedy funkcja zwróci 0 (0 < 1, prawda).

wynik = suma(5) = 5 + suma(4) = 5 + 4 + suma(3) = 5 + 4 + 3 + suma(2) = 5 + 4 + 3 + 2 + suma(1) =

5 + 4 + 3 + 2 + 1 + suma(0) = 5 + 4 + 3 + 2 + 1 + 0 = 15. 

Przykład 2

Wykonajmy zamianę liczby w systemie dziesiętnym na system dwójkowy. Algorytm jest wyjaśniony pod tym adresem.

Do rozwiązania problemu użyjemy rekurencji z nawrotami. Funkcja będzie wywoływać samą siebie, i w momencie gdy już "głębiej" się nie zagnieździ będzie powracać aby wykonać pozostałe instrukcje. Dzięki temu wypisane bity będą w prawidłowej kolejności.

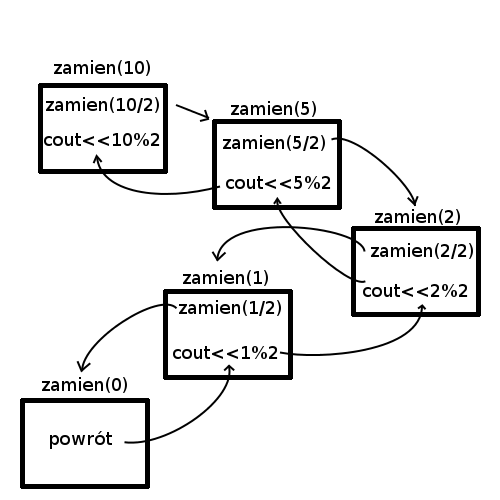
Rozwiązanie w C++

#include<iostream>
using namespace std;
 
void zamien(int n)
{
	//jesli n == 0 to zawracamy
	if(n==0)return;
	
	zamien(n/2); //zagnieżdżamy rekurencję
	
	cout<<n%2; //przy powrocie 
}
 
int main()
{
  	int n;
  	cout<<"Podaj liczbę naturalną: ";
  	cin>>n;
  	cout<<"Postać binarna liczby "<<n<<": ";
  	if(n==0) 
	  	cout<<0;
  	else 
	  	zamien(n);
  	
 	cout<<endl;
  	
  	return 0;
}

Przykładowe algorytmy, które są realizowane tą techniką:

• algorytm Euklidesa
• ciąg Fibonacciego
• wyszukiwanie binarne
• sortowanie szybkie
• sortowanie przez scalanie
• zamiana z dziesiętnego na dowolny inny system liczbowy
• przeszukiwanie w głąb
• podnoszenie do potęgi
• wypisanie wyrazu wspak
• silnia

Zobacz podobne:

• rekurencja zadania
• rekurencja ćwiczenia