Drzewo binarne

---

W tym artykule zajmiemy się pełnym drzewem binarnym zaimplementowanym na tablicy. Pokażę, w jaki sposób można się po nim przemieszczać oraz przedstawię przykładowe zadanie z rozwiązaniem.

Pojęcie drzewa binarnego

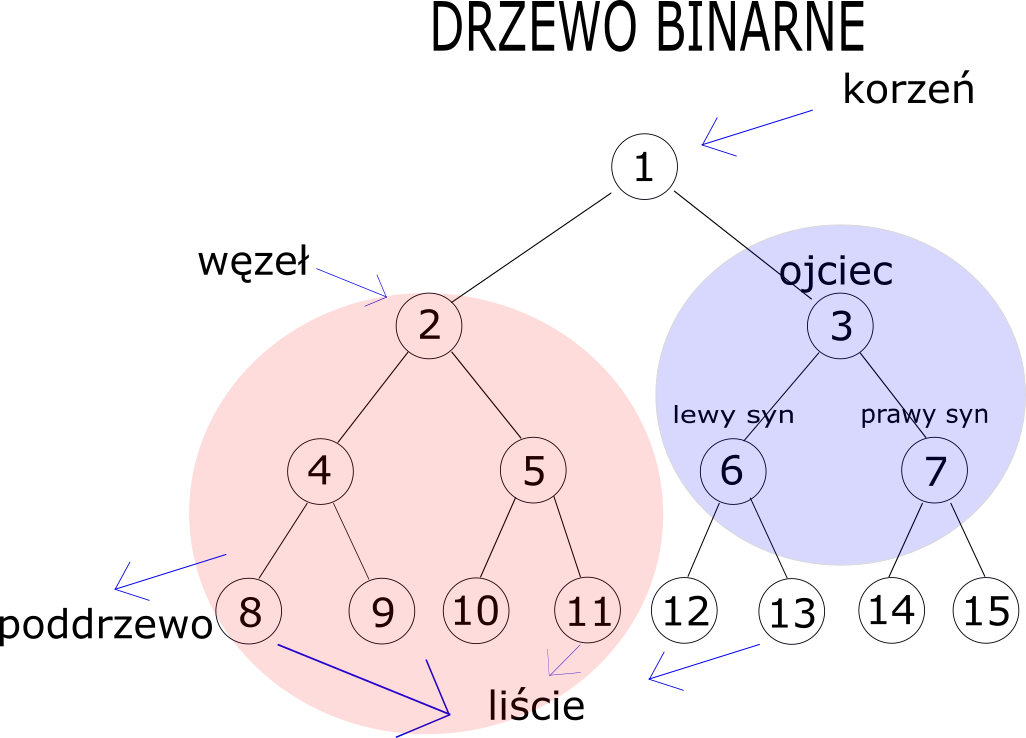
Drzewo binarne jest taką strukturą, w którym wyróżniamy wierzchołek będący na samej górze — korzeń drzewa, wierzchołki na samym dole — liście drzewa, a wszystkie wierzchołki nazywać będziemy węzłami. Jeśli weźmiemy dowolny wierzchołek (nie liść), to zauważymy, że ma on dwa połączenia znajdujące się tuż pod nim oraz jedno połączenie znajdujące się tuż nad nim. Wierzchołki znajdujące się pod nim nazywać będziemy jego synami, odpowiednio lewym i prawym synem, a on sam będzie dla nich ojcem.

Tworzenie pełnego drzewa binarnego.

W pierwszym kroku musimy określić z ilu poziomów będzie składać się nasze drzewo. Liczba komórek tablicy, jaka będzie potrzebna na budowę drzewa złożonego z n poziomów wynosi 2ⁿ - 1. Zatem, jeśli nasze drzewo będzie miało dziesięć poziomów, należy stworzyć tablicę wielkości 2¹⁰ - 1 = 1023, a najlepiej 2¹⁰ żeby móc wejść do komórki o indeksie 1023 (indeksujemy tablicę w C++ od 0).

Poruszanie się po drzewie w kierunku liść -> korzeń

Załóżmy, że jesteśmy w komórce tablicy o indeksie 11. Aby skoczyć jeden poziom wyżej, wystarczy na tej liczbie wykonać dzielenie całkowite przez 2: $$11 div 2 = 5.$$Czynność tę powtarzamy do mementu, aż indeks komórki tablicy osiągnie wartość 1.

żeby móc wejść do komórki o indeksie 1023 (indeksujemy tablicę w C++ od 0).

Poruszanie się po drzewie w kierunku korzeń -> liść

Będąc w wierzchołku reprezentującym korzeń (w komórce o indeksie równym 1), na samej górze drzewa, poruszając się w dół mamy dwa wyjścia, możemy przejść do lewego syna mnożąc wartość indeksu tablicy przez 2 lub przejść do prawego syna mnożąc indeks przez 2 i zwiększając go o 1.

Zadanie 1

Dla zadanych dwóch liczb całkowitych dodatnich nie większych niż bilion, reprezentującymi numery wierzchołków drzewa binarnego, określ jaka jest między nimi odległość. Przyjmij, że połączenie między dwoma węzłami jest równa 1.

Przykład 1 do zadania 1

Dane wejściowe

4 15

Dane wyjściowe

5

Przykład 2 do zadania 1

Dane wejściowe

7 12

Dane wyjściowe

3

Rozwiązanie

W tym zadaniu nie musisz tworzyć struktury drzewa binarnego w tablicy. Wystarczy, że zauważysz, w jaki sposób należy poruszać się po drzewie. Tak naprawdę, dla każdej iteracji, sprawdzamy, czy otrzymaliśmy tę samą wartość dla jednej i drugiej liczby. Jeśli nie, to przeskakujemy o poziom wyżej z tego wierzchołka, którego numer jest większy.

Rozwiązanie w C++

#include<iostream>
using namespace std;

int main()
{
	long long a, b; 
	int cnt = 0; //zmienna będzie zliczać odległość między wierzchołkami
	cout<<"Wprowadź numer pierwszego wierzchołka: ";
	cin>>a;
	cout<<"Wprowadź numer drugiego wierzchołka: ";
	cin>>b;
	
	while(a!=b)
	{
		if(a > b)	
			a/=2;
		else		
			b/=2;
		
		++cnt;
	}
	
	cout<<"Odległość między wierzchołkami wynosi "<<cnt;
	
	return 0;
}