Ćwiczenia iteracje

Ćwiczenie 1. Zrealizuj program, który dla dowolnej liczby naturalnej, określi ilość cyfr tej liczby.

Ćwiczenie 2. Zrealizuj program, który dla dwóch dowolnych liczb naturalnych a i b, podniesie a^b.

Ćwiczenie 3. Funkcja "gotoxy(x, y)" ustawia kursor tekstu w konsoli w miejsce x znaków od lewej strony oraz y znaków od góry (czyli w punkcie (x, y) zostanie wyświetlony tekst wygenerowany przez instrukcję "cout").

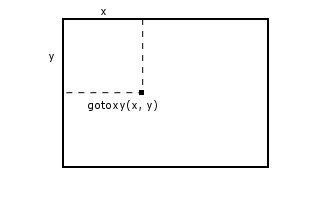
Dla podanej liczby naturalnej dodatniej, napisz program który narysuje figurę o boku n:

1. literę "O" o boku n.
2. literę "L" o bou n
3. literę "M" o boku n
4. literę "Z" o boku n
5. literę "X" o boku n
6. literę "R" o długości pionowej kreski równej 2n, i pozostałych bokach o długości n.

Jeśli funkcja gotoxy(int, int) nie działa, wpisz poniższy kod definiujący ją:

#include "windows.h"
void gotoxy(int x, int y)
{
	COORD c;
	c.X = x - 1;
	c.Y = y - 1;
	SetConsoleCursorPosition (GetStdHandle(STD_OUTPUT_HANDLE), c);
}

Ćwiczenie 4. Dla podanego n i m, gdzie n < m, wyświetl wszystkie liczby całkowite zawierające się w przedziale [n, m], spełniające warunek:

1. są nieparzyste lub podzielne przez 5
2. w dzieleniu przez 3 dają resztę 2 i cyfrą jedności jest 3 lub 4
3. dzielą się przez 5, ale nie dzielą się przez 3.

Ćwiczenie 5. Wartość funkcji trygonometrycznej sin(x) można wyznaczyć za pomocą szeregu Taylora:

$$sin(x) = x - \frac{x^3}{3 !} + \frac{x^5}{5 !} - \frac{x^7}{7 !} + ... = \sum_{n = 0}^{\infty} (-1)^n\frac{x^{2n + 1}}{(2n + 1)!} $$

Wykorzystując tą definicję napisz program, który policzy wartość funkcji trygonometrycznej dla argumentu x z dokładnością n, gdzie n oznacza ilość wyrazów w szeregu Taylora.

Ćwiczenie 6.  

Prezent - zadanie można testować na stronach: 

1. http://pl.spoj.com/WSDOCPP/problems/AL_03_08/
2. http://pl.spoj.com/problems/AL_03_08/

Święty Mikołaj z workiem prezentów odwiedził Jasia. Ponieważ Jasiu nie był do końca grzeczy, może sobie wybrać prezent, ale nie najdroższy. Wyjątkiem jest sytuacja, gdy w worku wszystkie prezenty są jednakowej wartości, wtedy Jasiu ma szczęście i może wybrać dowolny prezent. Mikołaj wyjmuje więc wszystkie prezenty, a Jasiu dokonuje najlepszego dla siebie wyboru - prezentu jak najbardziej wartościowego. Twoim zadaniem jest określić wartość prezentu jaki wybrał Jasiu.

Wejście

Ciąg liczb naturalnych określających wartości prezentów zakończony liczbą 0 (liczba 0 nie jest wartością prezentu). Wartosć prezentu nie przekracza 9*10⁸ oraz ilość prezentów jest mniejsza niż 3*10⁶.

Wyjście

Wartość prezentu Jasia.

Przykład

Input:
1 2 3 0

Output:
2

 Rozwiązania do ćwiczeń