Kurs maturalny z języka angielskiego!
kurs-maturalny-jezyk-angielski
PROGRAMOWANIE I ALGORYTMY
- Kurs języka Python
- Wstęp do Python
- Python — instrukcja warunkowa
- Python — pętle
- Python — napisy
- Python — listy — tablice jednowymiarowe
- Python — listy — tablice dwuwymiarowe
- Python — funkcje
- Python — krotki
- Python — słowniki
- Python — obsługa plików
- Python — rekurencja
- Moduły
- Algorytmy w Pythonie
- Z dziesiętnego na dowolny system liczbowy w Python
- Pierwiastki funkcji kwadratowej w Pythonie
- Suma cyfr w Pythonie
- Liczby doskonałe w Pythonie
- Pierwiastkowanie w Pythonie
- Ciąg Fibonacciego w Pythonie
- Czy pierwsza w Pythonie
- Faktoryzacja liczby w Pythonie
- Sito Eratostenesa w Pythonie
- Algorytm Euklidesa — Python
- Schemat Hornera w Python
- Potęgowanie szybkie w Pythonie
- Programowanie zachłanne, wydawanie reszty
- Czy palindrom w Pythonie
- Czy anagramy w Pythonie
- Szyfr Cezara w Python
- Wyszukiwanie wzorca w tekście — python
- Wyszukiwanie binarne w Pythonie
- Sortowanie bąbelkowe w Pythonie
- Sortowanie przez selekcję w Pythonie
- Sortowanie przez wstawianie w Pythonie
- Sortowanie przez scalanie w Pythonie
- Sortowanie szybkie w Pythonie
- Sortowanie kubełkowe w Pythonie
- Odwrotna Notacja Polska w Pythonie
- Bisekcja w Pythonie
- Z dziesiętnego na dowolny system liczbowy w Python
- Przydatne funkcje w Pythonie
- Zbiór zadań
- Suma dwóch liczb
- Zamiana wartości zmiennych
- Litery w przedziale
- Godziny i minuty
- Liczby w jednym wierszu
- Czy jesteś pełnoletni?
- Ciepło, zimno, gorąco
- Cyfra na tekst
- Maksymalna z trzech liczb
- Miejsca zerowe funkcji kwadratowej
- Suma n liczb
- Gwiazdkowy prostokąt
- Trzy razy dwa
- Liczby naprzemiennie
- Kolejne potęgi liczby 2
- Zamiana na duże
- Tyle samo zer i jedynek
- Zlicz wystąpienia słowa "oko".
- Zliczanie wystąpień liter
- Najdłuższy ciąg tych samych liter
- Dziedziczenie, pojazdy
- Dziedziczenie, osoby
- Suma dwóch liczb
- Kurs maturalny z informatyki
- Matura z informatyki
- Systemy liczbowe
- Struktury danych
- Arkusze maturalne
- Algorytmy maturalne
- Badanie czy liczba jest pierwsza
- Wyszukiwanie binarne
- Palindrom
- Wysz. wzorca w tekście
- Schemat Hornera
- Porządkowanie zbiorów
- Sortowanie bąbelkowe
- Sortowanie przez selekcję
- Sortowanie przez wstawianie
- Sortowanie przez scalanie
- Sortowanie kubełkowe
- Sortowanie szybkie
- Szyfrowanie
- Szyfr przestawieniowy
- Szyfr cezara
- Operacje na ułamkach
- NWW
- Przeszukiwanie z wartownikiem
- Lider w zbiorze
- Jednoczesne wysz. min. i max.
- Potęgowanie szybkie
- Połowienie przedziałów
- Metoda trapezów
- Metoda prostokątów
- Newton-Raphson
- Anagramy
- Liczby doskonałe
- Nierówność trójkąta
- Dwa odcinki
- Odwrotna notacja polska
- Rozkład liczby na czynniki
- Sito Eratostenesa
- Pozycyjne reprezentacje liczb
- Ciąg Fibonacciego
- Wyszukiwanie elementu min/max
- Elemement min. i maks.
- Algorytm Euklidesa
- Zadania - poziom podstawowy
- Zadania - poziom rozszerzony
- FRAKTAL
- Nagrody
- Edycja I
- Zadania z I Edycji
- Omówienie zadań I rundy
- Edycja II
- Zadania z II edycji
- Omówienie zadań z II edycji
- Edycja III
- Zadania z III edycji
- Omówienie zadań z III edycji
- Edycja IV
- Zadania z IV edycji
- Omówienie zadań IV rundy
- Edycja V
- Zadania z V edycji
- Edycja VI
- Zadania z VI edycji
- Edycja VII
- Zadania z VII edycji
- Edycja VIII
- Zadania z VIII edycji
- Omówienie zadań z VIII edycji
- Nagrody
- Rozwiązania zadań maturalnych
Zajęcia maturalne z informatyki
Olimpiada Informatyczna Juniorów
-
Prowadzący: Marcin Kasprowicz
- właściciel serwisu algorytm.edu.pl
- wrzesień 2024 — start zajęć
- czytaj więcej
Zadania z V edycji
FR_05_01 - Dzień tygodnia |
Dzień tygodnia
Wyznacz dzień tygodnia za n dni.
Dni tygodnia oznaczamy skrótami: Pn, Wt, Sr, Cz, Pt, So, Nd
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 1000) oznaczająca liczbę przypadków testowych. Każdy przypadek opisany jest w osobnym wierszu, na który składa się skrót dnia tygodnia i liczba n (1 ≤ n ≤ 109).
Wyjście
Dla każdego przypadku testowego wyznacz skrót dnia tygodnia, który nastąpi za n dni, licząc od dnia tygodnia podanego na wejściu.
Przykład
Wejście
4
Cz 1
Pt 2
So 3
Nd 4
Wyjście
Pt
Nd
Wt
Cz
FR_05_02 - Moc hasła |
Profesor Algobit zajmuje się szkoleniami na temat zabezpieczeń systemów informatycznych. Właśnie zakończył prowadzić kurs dla początkujących i przechodzi do sprawdzenia zdobytej wiedzy przez kursantów. Jedno z pytań brzmi następująco: "Podaj przykładowe hasło, które spełnia normy bezpieczeństwa systemu informatycznego". Z racji tego, że kursanci odpowiadają na pytania przy pomocy komputera, wykładowca używa do sprawdzania odpowiedzi specjalnej aplikacji, która sprawdza moc hasła.
Właśnie kończysz ten kurs i chcesz jak najlepiej wypaść na jego zaliczeniu, napisz więc program, który sprawdzi, czy podane hasło jest silne.
Uznajemy, że hasło jest silne jeśli ma co najmniej osiem znaków oraz zawiera znaki z każdej z czterech następujących kategorii:
- Wielkie litery: A, B, C, ..
- Małe litery: a, b, c, ...
- Cyfry: 0, 1, 2, ...
- Symbole występujące na klawiaturze (wszystkie znaki na klawiaturze niezdefiniowane jako litery lub cyfry) oraz spacje.
Wejście
W pierwszym wierszu jedna liczba określająca liczba haseł do przeanalizowania (n < 1001).
W kolejnych n wierszach hasło do przeanalizowania. Każde hasło jest złożone z co najwyżej 1000 znaków.
Wyjście
Na wyjściu powinny pojawić się tylko silne hasła w kolejności występowania na wejściu.
Przykład
Wejście: 3 pass1234 P@$$1234 Pa$$1234 Wyjście: Pa$$1234
FR_05_03 - Trójkąty |
Trój
Jasio jako bardzo zdolny uczeń postanowił uczęszczać na dodatkowe zajęcia z matematyki. Lekcje niezwykle mu się spodobały. Na koniec jednej z nich pani profesor przedstawiła zadanie domowe.
Narysowała na tablicy trójkąt równoboczny o boku=1. Następnie narysowała kolejny trójkąt równoboczny o boku=2 i podzieliła go na mniejsze części które były trójkątami równobocznymi o boku=1. Uczyniła to samo z kolejnym trójkątem. I zadała pytanie: ile wszystkich trójkątów możemy zaobserwować w trójkącie o boku n?

Jasio jest bardzo inteligentnym chłopcem i dość szybko wpadł na pomysł rozwiązania problemu. Wracając do domu rozmyślał jednak jak sprawdzić poprawność otrzymanych wyników. Ty jako starszy brat Jasia postanowiłeś pomóc mu w tym trudnym zadaniu.
Napisz program w którym określisz ile trójkątów można znaleźć w zadanym trójkącie o boku n.
Wejście:
W pierwszym wierszu jedna liczba k określająca ilość zestawów danych (k< 10^6).
Każdy zestaw składa się z jednej liczby n, przedstawiającej numer figury (0 ≤ n ≤ 10^9).
Wyjście:
Jedna liczba będąca odpowiedzią na zadane pytanie dla trójkąta o boku n. Wynik przedstaw modulo 10101.
Przykład:
Wejście: 3 1 2 10
Wyjście: 1 5 315
FR_05_04 - parkrun |
Parkrun
Parkrun to cykliczne biegi na dystansie 5 km z pomiarem czasu organizowane w każdą sobotę o godzinie 9:00. Biegi te przeznaczone są dla każdego bez względu na biegowy staż, uzyskiwane rezultaty, czy też wiek. Udział w biegach jest bezpłatny na podstawie jednorazowej rejestracji w systemie parkrun. Uzyskany kod uczestnika pozwala na udział w dowolnej liczbie biegów, w dowolnej lokalizacji parkrun na świecie. Wszelkie informacje o biegach parkrun organizowanych w Polsce, w tym ich lokalizacje, znajdziesz na stronie parkrun.pl.
Wystarczy promocji, czas na zadanie.
Jednym z zadań wolontariuszy biegów parkrun jest pomiar czasu na mecie, przypisanie pozycji uczestnikom i połączenie tych danych za pomocą kodów kreskowych. Niestety w ostatnim biegu pewnej lokalizacji nastąpiła awaria skanera i poproszono uczestników, aby przesłali swoje dane i uzyskane czasy na mecie. Moglibyśmy poprosić Ciebie, abyś wygenerował ranking na podstawie odtworzonej listy rekordów, ale tym problemem zajmie się Jasiu. Ty masz zadanie prostsze. Wyznacz imię i nazwisko uczestnika, który uzyskał najlepszy czas. Jeśli istnieje co najmniej dwóch uczestników o jednakowych najlepszych czasach ukończenia biegu, wypisz ich wszystkich w kolejności takiej, jakiej ich dane pojawiły się na wejściu.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita n (1 ≤ n ≤ 105) oznaczająca liczbę uczestników biegu. W kolejnych n wierszach znajdują się rekordy, w których podane są kolejno imię, nazwisko oraz czas ukończenia biegu w formacie MM:SS. Imie i nazwisko to ciągi małych i dużych liter alfabetu łacińskiego, których długość nie przekracza 20 znaków.
Wyjście
Na wyjściu należy podać imię i nazwisko uczestnika biegu, który uzyskał najlepszy czas. Jeśli istnieje co najmniej dwóch uczestników o jednakowych najlepszych czasach ukończenia biegu, wypisz wszystkich w kolejności takiej, jakiej ich dane pojawiły się na wejściu.
Przykład
Wejście
10
Adam Bak 22:52
Piotr Kakol 19:18
Marcin Kasprowicz 21:14
Mieczyslaw Bejnar 18:14
Mariusz Sliwinski 23:02
Witold Dlugosz 20:12
Maciej Boniecki 18:14
Arkadiusz Nowaczynski 19:59
Jaroslaw Konczak 22:00
Bartek Kraska 22:52
Wyjście
Mieczyslaw Bejnar
Maciej Boniecki
* zbieżność nazwisk w przykładowym wejściu przypadkowa.
FR_05_10 - Dzielniki dzielników |
Jasiu przeglądając stare notatki swojego dziadka Bajtomira zauważył pewien skomplikowany dla niego wzór:
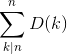
gdzie n ≥ 2 i należy do liczb całkowitych, a D(k) oznacza liczbę całkowitych dodatnich dzielników k.
Na przykład dla n = 72 nasz wzór ma postać:
D(1)+D(2)+D(3)+D(4)+D(6)+D(8)+D(9)+D(12)+D(18)+D(24)+D(36)+D(72)=
1+2+2+3+4+4+3+6+6+8+9+12=60
Jasiu mając daną liczbę podaną w postaci iloczynu różnych potęg liczb pierwszych chce poznać tę sumę, a ty musisz mu w tym pomóc :-)
Wejście
W pierwszym wierszu jedna liczba q określająca ilość zapytań (q < 105).
Specyfikacja każdego zapytania:
najpierw jedna liczba k określająca ilość liczb w postaci par ps, gdzie p to liczba pierwsza a s jej wykładnik, następnie w kolejnym wierszu k par liczb p i s (k < 10, p < 105, s < 11). Można założyć, że podstawy są prami różne.
Wyjście
Do każdego zapytania należy podać w oddzielnej linii szukaną sumę.
Przykład
Wejście: 1 2 2 3 3 2 Wyjście: 60
FR_05_05 - 1 2 3 |
Kombinatoryka jest działem w matematyce, w którym zadania z powodzeniem można rozwiązywać wykorzystując komputer. Dziś, tego pięknego kwietniowego dnia, przygotowałem dla Was jedno z nich. Napisz program, który stwierdzi ile różnych liczb n cyfrowych można zbudować z cyfr {1, 2, 3}, takich, że moduł (wartość bezwzględna) różnicy dwóch sąsiednich cyfr będzie zawsze równy jeden. Wynik przedstaw modulo 101010101.
Wejście
W pierwszym wierszu jedna liczba określająca liczbę zapytań (nie więcej niż milion).
Każde zapytanie składa się z jednej liczby naturalnej n określającej liczbę cyfr danej liczby (1 < n < 1000001).
Wyjście
Dla każdej liczby cyfr określ liczbę różnych liczb jaką można zbudować z cyfr {1, 2, 3}.
Przykład
Wejście: 2 2 3 Wyjście: 4 6
Wyjaśnienie
Dla liczby złożonej z 3 cyfr (drugi przykład) możemy zbudować następujące liczby: 121, 123, 212, 232, 321, 323,
FR_05_06 - StarWars |
StarWars
Nadchodzi kolejny piękny słoneczny dzień na planecie Tatooine. Beru i Owen bawią się z Lukem w chowanego. Luke świadomy swojego zwycięstwa próbuje dać szanse wujostwu i przed ukryciem daje im tajemniczą kartkę, na której zapisał współrzędne skraplaczy wilgoci w przestrzeni dwuwymiarowej z dopiskiem „Kolejna wskazówka znajduje się w przestrzeni ograniczonej największą możliwą figurą utworzoną z dowolnej ilości punktów podanych wyżej". Wujostwo zastanawia się jak duży może być to obszar. Będąc ich przyjacielem oraz fanem Gwiezdnych Wojen pomóż im wyznaczyć ten obszar. Podaj pole i obwód utworzonej w ten sposób figury.
Uwaga! Odległość pomiędzy każdymi dwoma skraplaczami należy zaokrąglić do dwóch miejsc po przecinku.
Wejście:
W pierwszej linii jedna niewielka liczba (n<1001) oznaczająca liczbę przypadków testowych.
W drugiej linii jedna liczba t (t<10001) oznaczająca liczbę skraplaczy wilgoci na farmie.
W kolejnych t liniach dwie liczby x,y będące współrzędnymi skraplaczy (|x|,|y|<1001)
Wyjście:
Dwie liczby oddzielone spacją, pierwsza będąca obwodem figury natomiast druga wyrażająca pole tej figury. Przyjmujemy, że długość pojedynczego punktu jest odcinkiem o długości 0.
Wynik zaokrąglamy do dwóch miejsc po przecinku. Zer nie znaczących nie wyświetlamy.
Przykład:
Wejście: 3 6 -1 1 2 -1 0 -1 1 1 2 2 -1 -3 4 0 0 5 5 0 5 5 0 1 2 2
Wyjście: 13.77 10.5 20 25 0 0
Rysunek pomoniczy do zadania:

Wyjaśnienie do przykładu pierwszego:
Obwód=3.16+3+3.61+4=13.77
Pole=3*5-(1*3/2)-(2*3/2)=10.5
FR_05_07 - Zagadka |
Zagadka
Tu powinna być jakaś historyjka, ale jej nie będzie. W zamian dostaniesz dwa rysunki, które musisz powiązać z przykładami wejścia/wyjścia, i przy pomocy specyfikacji wejścia/wyjścia napisać program rozwiązujący tę zagadkę.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 100) oznaczająca liczbę przypadków testowych. Każdy przypadek testowy opisują, w pierwszym wierszu jedna liczba całkowita n (1 ≤ n ≤ 104) oznaczająca długość ciągu liczb całkowitych. W wierszu drugim danych jest n liczb całkowitych ai (1 ≤ ai ≤ 1000) uporządkowanych nierosnąco.
Wyjście
Dla każdego przypadku testowego należy wypisać nierosnący ciąg liczb całkowitych.
Przykład
Wejście
2
5
6 4 4 3 1
4
7 5 3 2
Wyjście
5 4 4 3 1 1
4 4 3 2 2 1 1
FR_05_08 - Metrowiec 2 |
Firma "Metrax" zajmuje się wypiekaniem oraz sprzedażą pysznego ciasta zwanego metrowcem. We firmowym piecu można wypiec ciasto o długości n centymetrów. Ciasto może być pocięte na różnej długości kawałki. Najkrótszy może mieć długość 1cm a najdłuższy może mieć długość całego ciasta czyli n cm. Wiadomo, że cena ciasta o długości x może się różnić od ceny ciasta o długości y. Twoim zadaniem jest określenie, ile firma "Metrax" może zarobić najwięcej przy minimalnej liczbie kawałków.
Wejście
W pierwszym wierszu jedna liczba t określająca liczbę zestawów danych (t < 101).
Specyfikacja każdego zestawu danych.
W pierwszym wierszu jedna liczba n określająca długość metrowca (n < 1001).
W drugim wierszu n liczb z zakresu [1..1000] takich, że i-ta liczba określa zarobek za ciasto o długości i.
Wyjście
Dla każdego zestawu po dwie liczby. Pierwsza określa maksymalny zarobek, jaki uzyska firma "Metrax", druga minimalną liczbę kawałków.
Przykład
Wejście: 3 5 1 1 4 7 7 5 1 1 3 4 4 6 1 2 3 3 3 4 Wyjście: 8 2 5 2 6 2
FR_05_09 - Obwód prostokąta |
Obwód prostokąta
Dla danej wartości n wyznacz minimalną wartość obwodu prostokąta o całkowitych bokach, którego powierzchnia wynosi n.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 1000) oznaczająca liczbę przypadków testowych. Każdy przypadek testowy, to jedna liczba całkowita n (1 ≤ n ≤ 109) oznaczająca wartość powierzchni prostokąta.
Wyjście
Dla każdego przypadku należy wypisać minimalną wartość obwodu dla prostokąta o całkowitych bokach, którego powierzchnia wynosi n.
Przykład
Wejście
3
1
2
3
Wyjście
4
6
8
FR_05_11 - Podbiegi |
Podbiegi
Jasiu trenuje dzisiaj kilkuminutowe podbiegi. W tym celu zaplanował sobie trasę z kolejnymi wysokościami chwilowego postoju na odpoczynek. Zauważył jednak, że w niektórych przypadkach, jeśli zmieni kolejność punktów wysokości postoju, to liczba podbiegów będzie większa, a na tym mu najbardziej zależy. Znając ciąg wartości wysokości, przegrupuj kolejność interwałów biegowych tak, aby uzyskać maksymalną liczbę podbiegów.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 1000) oznaczająca liczbę przypadków testowych. Dla każdego przypadku, w pierwszym wierszu znajduje się liczba całkowita n (2 ≤ n ≤ 1000) oznaczająca liczbę punktów postoju. W wierszu drugim danych jest n liczb całkowitych ai (0 ≤ ai ≤ 1000) oznaczających wartości wysokości postoju.
Wyjście
Dla każdego przypadku testowego należy podać maksymalną liczbę podbiegów, w wyniku optymalnego przegrupowania kolejności wartości wysokości postoju.
Przykład
Wejście
2
4
20 10 30 10
5
20 30 10 0 40
Wyjście
2
4
Wyjaśnienie: W pierwszym przypadku Jasiu może uzyskać maksymalnie dwa podbiegi zmieniając kolejność wyrazów w ciągu na np. 10 20 10 30 lub 10 10 20 30. W drugim przypadku istnieje tylko jedna kombinacja 0 10 20 30 40, dla której maksymalizujemy liczbę podbiegów do czterech.
FR_05_13 - Malowanie |
Malowanie
Drewniany płot ogrodzeniowy u Jasia trzeba koniecznie odrestaurować. Sztachety wyblakły i należy ponownie pokryć je farbą. Jasiu chce zachować liczbę dotychczasowych kolorów sztachet na przęsłach, ale postanowił, że sąsiednie sztachety muszą różnić się barwą. Mógłby malować sztachety na przemian i uzyskałby zamierzony efekt, ale zmiana koloru sztachety na inny powoduje dodatkowe koszty, bo sztachetę taką trzeba malować dwukrotnie. Należy zminimalizować koszty, czyli wyznaczyć najmniejszą liczbę sztachet w przęśle, których barwa zostanie zmieniona na inną, ale taką, która znajdowała się w palecie barw danego przęsła. Wyjątkiem są przęsła zabarwione jednym kolorem, w tym przypadku co druga sztacheta zostanie pomalowana nową barwą.
W celu wyznaczenia sztachet do przebarwienia, Jasiu opisał każde z przęseł za pomocą ciągu dużych liter, gdzie jednakowym literom odpowiada jednakowa barwa, a różnym literom - różna barwa sztachety. Na podstawie tych danych należy wyznaczyć najmniejszą możliwą liczbę sztachet, których barwę należy zmienić.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita p (1 ≤ p ≤ 100) oznaczająca liczbę przęseł płotu. Każde przęsło opisuje w osobnym wierszu ciąg dużych liter alfabetu łacińskiego, którego długość zawiera się w przedziale [1, 106]. Każdej literze ciągu przyporządkowany jest kolor sztachety, gdzie jednakowym literom odpowiada jednakowa barwa. Rozmiar plików wejściowych nie przekracza 5 MB.
Wyjście
Dla każdego ciągu reprezentującego przęsło, należy wypisać najmniejszą liczbę sztachet, które należy przebarwić zgodnie z wytycznymi Jasia.
Przykład
Wejście
5
TOO
ABBA
YYYYY
XXYYZZ
FRAKTAL
Wyjście
1
2
2
3
0
Wyjaśnienie.
Pierwsze przęsło TOO ma trzy sztachety zabarwione dwoma różnymi kolorami. Dwa pierwsze sztachety wystarczy pomalować tym samym kolorem, a kolor ostatniej sztachety należy zmienić na T, aby spełnione zostały warunki. Przęsło drugie ABBA ma cztery sztachety i dwie barwy. Mamy tu dwie kombinacje końcowe, albo ABAB albo BABA, co w obu przypadkach oznacza zmianę barwy dwóch sztachet. Przęsło trzecie to wyjątek, tutaj dobieramy nową barwę minimalnie dla dwóch sztachet i kolorujemy całe przęsło np. na YAYAY. Czwarte przęsło wymaga przebarwienia minimum trzech sztachet, można to zrobić na kilka sposobów, np. XZYXZX. Przęsło FRAKTAL, jak widać, nie potrzebuje zmiany barw sztachet, wystarczy je tylko odświeżyć, malując na ten sam kolor.
FR_05_14 - Miasta |
Wypisz miasto, które jest n-te z kolei co do wielkości. Jeśli jest kilka takich miast wypisz je w porządku alfabetycznym (miasta o tej samej nazwie traktujemy jako dwa różne miasta). Jeśli takich miast nie ma, wypisz napis BRAK.
Wejście
W pierwszym wierszu jedna liczba n określająca liczbę miast (n < 100 001)
W kolejnych n wierszach nazwy miast oraz liczba ludności (nazwa miasta jest nazwą złożoną z co najwyżej 23 dużych liter języka łacińskiego, ludność to liczba całkowita mieszcząca się w przedziale [103..109])
Następnie jedna liczba q - liczba zapytań (q < 100 001).
Każde zapytanie składa sie z jednej liczby całkowitej należącej do przedziału [1..n] określające, które miasto pod względem wielkości należy podać.
Wyjście
Dla każdego zapytania miasta wypisane w jednym wierszu oddzielone znakiem spacji w porządku alfabetycznym lub napis BRAK, jeśli nie ma takiego miasta.
Przykład
Wejście: 5 WARSZAWA 1700000 TORUN 210000 OLSZTYN 170000 DZIALDOWO 21000 BAJTOCJA 21000 3 1 4 5 Wyjście: WARSZAWA BAJTOCJA DZIALDOWO BRAK
FR_05_15 - Wielokąt foremny |
Wielokąt foremny
Na okręgu rozmieszczono równomiernie punkty i oznaczono je losowo A lub B. Twoim zadaniem jest stwierdzić, czy istnieje co najmniej jeden wielokąt foremny, którego wierzchołkami są wyłącznie punkty A należące do okręgu.
Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 100) oznaczająca liczbę przypadków testowych. Każdy przypadek testowy, to ciąg złożony z liter A lub B, którego długość zawiera się w przedziale [3, 106]. Kolejność liter oznacza kolejne punkty na okręgu. Rozmiar plików wejściowych nie przekracza 5 MB.
Wyjście
Na wyjściu, dla każdego przypadku testowego należy wypisać słowo TAK, jeśli z punktów na okręgu oznaczonych literą A, można zbudować co najmniej jeden wielokąt foremny, albo słowo NIE w przeciwnym przypadku.
Przykład
Wejście
4
AAA
AABA
ABABA
ABAAAB
Wyjście
TAK
NIE
NIE
TAK
FR_05_16 - Stos i arytmetyka |
W tym zadaniu zajmiemy się bardzo ciekawym sposobem wykonującym obliczenia arytmetyczne bez użycia nawiasów i wykorzystując strukturę danych jaką jest stos.
Zaczniemy od przykładu. Wyznaczmy wynik działania
(3+4)*(5+6) = 77.
W klasycznym zapisie wykorzystaliśmy nawiasy. W notacji, którą tu przedstawię, podane wyrażenie może wyglądać następująco:
3 4 + 5 6 + * = 77
A oto algorytm:
- Powtarzaj dopóki są dane do wczytania
- Jeśli wczytany obiekt jest liczbą, to wrzuć ją na stos
- Jeśli wczytany obiekt jest operatorem, to
- Zdejmij pierwszą liczbę ze stosu i zapisz ją pod zmienną x
- Zdejmij drugą liczbę ze stosu i zapisz ją pod zmienną y
- Wykonaj działanie: y operator x i wynik wrzuć na stos
- Wypisz wartość, która została na stosie
Na wejściu pojawi się ciąg liczb i operatorów zapisanych poprawnie w omawianej notacji. Twoim zadaniem jest wyliczenie wartości wyrażenia, wypisanie wyniku oraz nazwę algorytmu złożonego z trzech dużych liter.
Wejście
W pierwszym wierszu jedna liczba q określająca liczbę elementów wyrażenia zapisanego w pewnej notacji (nie więcej niż 100).
Każde z q wierszy ma postać. Najpierw jedna liczba należąca do zbioru {0, 1}. Jeśli pojawi się 1, to następnie pojawi się niewielka całkowita liczba, którą należy wrzucić na stos, w przeciwnym razie pojawi się operator należący do zbioru {+, -, *, /}. Dane są tak dobrane, aby wynik był zawsze całkowity.
Wyjście
Wyjście składa się z dwóch wierszy. W pierwszym wierszu wartość wyrażenia, natomiast w drugim trzyliterowa nazwa omawianego algorytmu zapisana z dużych liter w języku polskim.
Przykład
Wejście: 7 1 3 1 4 0 + 1 5 1 6 0 + 0 * Wyjście: 77 *** Zamiast gwiazdek należy wpisać nazwę algorytmu.
FR_05_17 - Ogród Jasia III |
Ogród Jasia III
Jak co roku, ogród Jasia wiosną nabiera kolorów. Tym razem Jasiu postanowił, że dwa zraszacze umiejscowi w pewnym stałym miejscu i to one będą nawadniać wszystkie kwiaty w ogrodzie. Regulacja siły (długości promieni) nawadniania dwóch zraszaczy będzie regulowana za pomocą ciśnienia. Trzeba więc tak dobrać długości promieni działania dwóch zraszaczy, aby ich suma długości była jak najmniejsza, i jednocześnie powierzchnia nawadnianego obszaru możliwie najmniejsza, bo to pozwoli zaoszczędzić hektolitry wody. Znając współrzędne wszystkich kwiatów w ogrodzie, pomóż Jasiowi i oblicz sumę długości promieni działania dwóch zraszaczy.
Wejście
W pierwszym wierszu wejścia znajduje się pięć liczb całkowitych n, x1, y1, x2, y2 (2 ≤ n ≤ 1000, -104 x1, y1, x2, y2 ≤ 104), gdzie n to liczba kwiatów w ogrodzie, a x1, y1, x2, y2, to współrzędne całkowite dwóch zraszaczy. Dalej w nwierszach podane są współrzędne kwiatów, w każdym wierszu dwie liczby całkowite x, y (-104 ≤ x, y ≤ 104). Należy założyć, że żadne dwa kwiaty nie rosną w tym samym miejscu.
Wyjście
Na wyjściu należy wypisać najmniejszą sumę długości promieni działania dwóch zraszaczy, z dokładnością do co najmniej dwóch cyfr po przecinku, obejmujących swoim zasięgiem wszystkie kwiaty w ogrodzie.
Przykład
Wejście
4 2 1 7 1
11 5
6 4
1 1
3 5
Wyjście
6.66
FR_05_18 - Curling v2! |
Curling v2
Pewnego dnia Jasiowi bardzo się nudziło i postanowił pooglądać TV. Po żmudnej wędrówce po kanałach napotkał transmisję zawodów gry w Curling. Jasiu zaciekawiony nowo poznaną dyscypliną sportową postanowił zagrać ze znajomymi w grę o podobnych zasadach.
Zasady gry:
- W grze biorą udział dwie drużyny.
- Każda drużyna ma do dyspozycji tyle samo kamieni.
- Grę zawsze zaczyna drużyna czerwona.
- Ruchy odbywają się na przemian.
- Rozgrywana będzie zawsze dokładnie jedna runda, która kończy się wraz z wyrzuconym ostatnim kamieniem drużyny żółtej.
- Drużyna przed wykonanym rzutem ma wybór z którego miejsca (p) o współrzędnych (p,-11), gdzie (-2<=p<=2),
będzie rzucać swój kamień.
- Wyrzucony kamień z miejsca p może trafić w sektor osi OX z przedziału [5*p-5,5*p+5]
- Przed rzutem drużyna podaje w które miejsce chce oddać swój rzut.
- W przypadku, gdy cel nie zawiera się w możliwym sektorze drużyna traci swój rzut.
- Zakłada się, że przynajmniej jeden kamień trafi w dom, który jest kołem o równaniu x^2+y^2=100.
- Zwycięża ta drużyna, która umieści swój kamień bliżej środka koła.
- W przypadku remisu żadna z drużyn nie jest zwycięzcą.
- W przypadku gdy wyrzucony kamień na swojej drodze do celu napotyka inny kamień dochodzi do zderzenia.
- Podczas zderzenia kamień uderzający zatrzymuje się na pozycji uderzanego. Natomiast uderzany przeskakuje w zależności od miejsca (p) uderzającego zawsze o 1 jednostkę na osi OY do przodu oraz o +|p| jednostek na OX, jeśli współrzędna x osiągnięta w momencie zderzenia jest większa od miejsca wyrzutu lub o -|p| w zdarzeniu przeciwnym.
- Zakłada się, że występują tylko zderzenia centralne, a każde uderzenie z p równego 0 jest poprawnie rozpatrzone według powyższych reguł.
- W przypadku napotkania innego kamienia przez uderzony już wcześniej kamień stosuje się przeskok analogiczny do wyżej opisanych reguł za wyjątkiem (p), które zawsze pochodzi od rzutu wywołującego ciąg zderzeń.
Wejście:
W pierwszym wierszu znajduje się mała liczba nieparzysta k oznaczająca ilość wyrzuconych kamieni .
W kolejnych k wierszach znajdują się 3 liczby x,y,p. Pierwsza i druga oznacza współrzędne celu kamienia podane przez drużynę i miejsce p, z którego został kamień wyrzucony. |X|<16,(-10<=Y<=16).
W kolejnym wierszu znajduje się liczba t określająca liczbę zapytań. (1<=t<=10^6)
W następnych t wierszach znajdują się 3 liczby x,y,p oznaczające pierwszą i drugą współrzędną będącą celem ostatniego kamienia drużyny żółtej i miejsce, z którego drużyna rzuca swój ostatni kamień.
Wyjście:
Odpowiedź „TAK”, jeżeli wygra drużyna żółta, w przeciwnym wypadku „NIE”. Dodatkowo, jeśli „TAK”, należy podać ilość punktów w nawiasie kwadratowym, które definiowane są jako 1 punkt za każdy kamień zwycięskiej drużyny leżący bliżej od najbliżej położonego względem środka koła kamienia drużyny przeciwnej.
Przykład:
Wejście: 5 -2 0 0 -1 0 -1 0 -7 1 -1 -3 1 -1 -3 1 3 0 0 0 0 0 1 0 0 2
Wyjście: TAK [1] TAK [2] TAK [1]
Wytłumaczenie przeskoków dla kamyka na (-5.0):
a) Uderzonego przez inny kamyk z p=0. (-5.0)->(-5.1)
b) Uderzonego przez inny kamyk z p=-2. (-5.0)->(-7.1)
c) Uderzonego przez inny kamyk z p=1. Rzut niemożliwy
Wytłumaczenie przykładu:
Sytuacja przed zapytaniami:

Sytuacja po zapytaniu pierwszym:

Sytuacja po zapytaniu drugim:


FR_05_19 - Równanie kwadratowe z wartością bezwzględną |
Rozwiąż równanie:
ax2 + b|x| + c = 0
Wejście
W pierwszym wierszu jedna liczba t określająca liczbę zestawów danych (t < 106).
W kolejnych t wierszach po trzy liczby całkowite a, b oraz c, gdzie każda mieści się w przedziale [-1000..1000]
Wyjście
Dla każdego zestawu testowego napis brak, gdy równanie nie ma rozwiązań, napis nieskonczenie wiele, jeśli rozwiązań jest nieskończenie wiele oraz rozwiązania wypisane w szyku rosnącym z dokładnością do sześciu miejsc po przecinku.
Przykład
Wejście: 3 0 1 -1 0 1 1 0 0 0 Wyjscie: -1.000000 1.000000 brak nieskonczenie wiele
FR_05_20 - Mainframe |
Firma "FRAKTAX" ma do wykonania bardzo ważne zadanie i musi korzystać z usług superkomputera. Superkomputer można rezerwować jedynie na cały dzień i nikt inny w tym czasie nie ma do niego dostępu. Wiadomo także, że ta super maszyna w ciągu jednego dnia poradzi sobie z każdym zadaniem. Bywa często tak, że pracownicy firmy, muszą ustawiać się w kolejce rezerwując kolejne dni. Okazuje się jednak, że w skutek złego planowania, firma nie realizuje swoich zleceń w terminowym czasie, za co ponosi kary pieniężne. Znając terminy na wykonanie zadań oraz kary za ich przekroczenie, określ, jaką najmniejszą karę może zapłacić firma.
Wejście
W pierwszym wierszu jedna liczba t określająca liczbę zestawów testowych (nie więcej niż 100).
Specyfikacja każdego zestawu testowego.
W pierwszym wierszu jedna liczba n określająca liczbę zadań (n < 100001).
Każde zadanie składa się z terminu p na zadanie oraz kary k za przekroczenie tego terminu (p ∈ [1..n], k ∈ [1..100000]).
Wyjście
Dla każdego zestawu minimalna kara, jaką firma FRAKRAX może zapłacić za niedotrzymanie terminów.
Przykład
Wejście: 1 7 2 60 4 50 4 70 6 10 4 20 1 30 3 40 Wyjście: 50
