Zadania - III edycja

---

powrót

Palindromes

Palindrom to takie wyrażenie, które czytane od lewej do prawej brzmi tak samo jak czytane wspak, na przykł‚ad:

kajak

Dla danego wyrazu okreś›l minimalną… liczbę™ znaków jaką… należy podmienić‡ aby powstał‚ palindrom.

Wejście

 

W pierwszym wierszu jedna liczba okreś›lają…ca liczbę™ zestawów danych.

Każdy zestaw skł‚ada sią™ z mał‚ych lub dużych liter ję™zyka ł‚aciń„skiego, nie dł‚uższy niż 1000 znaków.

 

Wyjście

Dla każdego zestawu wypisz minimalną… liczbę™ zamian znaków, aby powstał‚ palindrom.

Uwaga!

Zakł‚adamy, że aby powstał‚ palindrom, wielkość‡ znaków jest bez znaczenia.

Przykład

Wejś›cie:
3
Kajak
Lokomotywa
fraktal

Wyjście:
0
5
3

---

 

Lokata

Jasiu, główny informatyk banku, dostał nowe zadanie do wykonania. Musi napisać funkcję, która pomoże określić jak długo klient będzie musiał czekać, aby pomnożyć swoje kapitały inwestując je na lokacie. Klient podaje pewną kwotę i deklaruje kwotę, którą chciałby otrzymać, a program przy danej stopie procentowej musi poinformować klienta, po upływie jakiego czasu będzie mógł on cieszyć się z kapitału i zysku, który kapitalizowany jest corocznie. Teraz wystarczy napisać taki moduł i gotowe. Pewnie już się domyślasz, że Jasiu nie ma czasu i potrzebuje pomocy. Napisz więc program, który na podstawie kapitału początkowego i końcowego oraz stopy procentowej wyznaczy czas trwania lokaty.


Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (0 < d < 1000) oznaczająca liczbę zestawów danych. W kolejnych wierszach znajdują się zestawy danych. Każdy zestaw składa się z trzech liczb rzeczywistych a, b, p (0 < a < b < 109, 0 < p < 100) podanych z dokładnością do dwóch cyfr po przecinku. Liczba a oznacza kapitał początkowy, liczba b - kapitał końcowy, liczba p to roczna stopa procentowa.

Wyjście
Na wyjściu należy wypisać d wierszy, w każdym wierszu jedna liczba rzeczywista zaokrąglona do co najmniej trzech cyfr po przecinku oznaczająca czas trwania lokaty wyrażony w latach.


Przykład

Wejście
2
100.00 200.00 5.00
1000.00 1100.00 5.00

Wyjście
14.207
1.953

---

Zbior liczb niepodzielnych

 

Z danego przedział‚u [a..b] naleźy wypisać‡ ile jest liczb naturalnych dodatnich, które nie dzielą… się™ przez źadną… liczbę™ z multizbioru A = {a1, a2, ..., an}.

Wejś›cie

W pierwszym wierszu jedna liczba n okreś›lająca ilość‡ elementów multizbioru A (n ≤ 10000).

W drugim wierszu n liczb multizbioru. Kaźda z nich mieści się™ w przedziale [1..106].

W trzecim wierszu jedna liczba q oznaczają…ca liczbę™ zapytań„ (q ≤ 10000).

Kaźde zapytanie jest reprezentowane przez dwie liczby a i b określają…ce przedział w postaci [a..b], gdzie a ≤ b oraz a, b ∈ [1..106].

Wyjś›cie

Dla każdego zapytania wypisz liczbę™ liczb niepodzielnych przez żadną… liczbę z multizbioru A.

Przykł‚ad

Wejście:
3
2 3 4
2
1 10
10 20

Wyjś›cie:
3
4

---

 

Desant

Na poligonie odbywają się bardzo ważne dla obronności kraju ćwiczenia - nocny desant. Każdy spadochroniarz po wylądowaniu musi zgłosić współrzędne kwadratu, w którym wylądował, w ten sposób do dowódcy docierają wszystkie współrzędne kwadratów, na których wylądował co najmniej jeden żołnierz. Po zakończonym desancie dowódca chciałby wiedzieć, czy na kwadratach o strategicznym znaczeniu, wylądował choćby jeden spadochroniarz. W tym celu do systemu trzeba dodać kolejną funkcję, która szybko i bezbłędnie odpowie na zapytania dowódcy.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita n (1 ≤ n ≤ 5 · 105) oznaczająca liczbę spadochroniarzy biorących udział w desancie. W kolejnych nwierszach podane są po dwie liczby całkowite, x, y (0 ≤ x, y ≤ 106) oznaczające współrzędne lądowań kolejnych żołnierzy. W następnym wierszu znajduje się liczba całkowita q (1 ≤ q ≤ 104) oznaczająca liczbę zapytań dowódcy. W kolejnych q wierszach podane są po dwie liczby całkowite, x1, y1 (0 ≤ x1, y1 ≤ 106) oznaczające współrzędne kwadratów o strategicznym znaczeniu.

Wyjście
Dla każdego zapytania należy wypisać słowo TAK, jeśli w kwadracie o strategicznym znaczeniu wylądował co najmniej jeden żołnierz, albo słowo NIE w przeciwnym przypadku.

Przykład

Wejście
5
1 3
4 2
3 5
1 1
1 1
3
3 1
4 2
0 2

Wyjście
NIE
TAK
NIE

---

Zarobek doskonały

Żadna praca nie hań„bi, a szczególnie ta, w której można dobrze zarobić. W pewnej firmie "Bittext" oferującej usługi programistyczne, wysokość poborów jest uzależniona od iloś›ci poprawek i błędów programisty. W skrajnej sytuacji programista może popełnić‡ tak dużo błędów, że jego zarobek w cią…gu dnia bę™dzie ujemny (pracownik bę™dzie musiał‚ zapłacić‡ firmie daną kwotę). Na szcz궛cie firma jest wyrozumiał‚a i pozwala swoim pracownikom dobrać spójny podcią…g dni w danym okresie, z którego będą wypłacane profity. Może się™ okazać‡, że do wypłaty będzie brany tylko jeden dzień„. Twoim zadaniem jest okreś›lenie optymalnej wartoś›ci, którą… powinien wziąć‡ pod uwagę™ programista na przestrzeni n dni.

Wejście

W pierwszym wierszu jedna niewielka liczba określająca liczbę™ zastawów danych.

Każdy zestaw skł‚ada się z dwóch wierszy. Pierwszy określa liczbę™ dni branych pod uwagę™ do wypłaty (liczba ta jest nie wię™ksza niż 105). W drugim wierszu dla każdego dnia wartość‡ zarobionej kwoty mieszczą…cej się™ w przedziale [-20000..20000].

Wyjś›cie

Dla każdego zestawu danych jedna liczba określają…ca maksymalny zarobek pracownika.

Przykład

Wejś›cie:
1
6
-1 -3 6 -5 6 1

Wyjście: 

8 

---

 

Stronicowanie

Wyobraź sobie, że jesteś programistą w pewnej firmie i jest piątek popołudnie. Przed wyjściem robisz ostatnie porządki na biurku aż tu nagle ni stąd, ni zowąd pojawia się dyrektor. Z jakiegoś powodu nikt nie napisał programu, który miał być gotowy na wczoraj. Ponieważ nikogo oprócz Ciebie już nie ma, więc wiesz już co będziesz robił w piątek wieczorem. Twoje zadanie, to napisać skrypt, który będzie odpowiedzialny za stronicowanie rekordów i wyświetlanie ich na stronie w sposób zgodny ze specyfikacją podaną przez klienta. Skrypt powinien wyświetlać rekordy w odwrotnej kolejności ich zapisywania i grupować je pewnymi porcjami, a ponadto wyświetlać odnośniki do pierwszej i ostatniej strony oraz do trzech stron w przód i do trzech stron w tył, licząc od strony bieżącej, o ile takie istnieją. Na potrzeby testów musisz napisać program, który będzie pobierał rekordy i wyświetlał je odpowiednio na stronie w zależności od zapytania o numer strony.

Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite r, w (0 < r < 100000, 0 < w < 100000) oznaczające odpowiednio liczbę rekordów w bazie danych oraz liczbę rekordów wyświetlanych na stronie. W kolejnych r wierszach podane są ciągi znaków złożone z małych i wielkich liter alfabetu łacińskiego, cyfr i znaku spacji, o maksymalnej długości 100. Każdy taki ciąg jest kolejnym rekordem zapisanym w bazie danych. Dalej znajduje się liczba całkowita q (0 <q < 1000) oznaczająca liczbę zapytań, po której znajduje się q liczb całkowitych k (0 < k < 100000), każda liczba w osobnym wierszu oznaczająca zapytanie o numer strony.

Wyjście
Dla każdego zapytania należy wypisać odpowiednią liczbę rekordów na stronie k-tej, każdy rekord w osobnym wierszu, oraz w nowym wierszu ciąg odnośników do kolejnych stron, według specyfikacji. Wszystkie numery reprezentujące odnośniki, poza bieżącą stroną, zapisywane są w kwadratowym nawiasie []. Jeśli liczba k (bieżąca strona) pomniejszona o 4 jest większa od 1 lub liczba k powiększona o 4 jest mniejsza od wartości ostatniej strony, należy odpowiednio po pierwszej stronie lub przed ostatnią stroną wstawić trzy kropki. Separatorem pomiędzy odnośnikami jest co najmniej jedna spacja. W przypadku zapytania wykraczającego poza zakres ostatniej strony należy wypisać: HTTP 404
Pomiędzy zapytaniami dozwolony jest dodatkowy znak końca linii.

Przykład

Wejście
37 3
rekord nr 1
rekord nr 2
rekord nr 3
rekord nr 4
rekord nr 5
rekord nr 6
rekord nr 7
rekord nr 8
rekord nr 9
rekord nr 10
rekord nr 11
rekord nr 12
rekord nr 13
rekord nr 14
rekord nr 15
rekord nr 16
rekord nr 17
rekord nr 18
rekord nr 19
rekord nr 20
rekord nr 21
rekord nr 22
rekord nr 23
rekord nr 24
rekord nr 25
rekord nr 26
rekord nr 27
rekord nr 28
rekord nr 29
rekord nr 30
rekord nr 31
rekord nr 32
rekord nr 33
rekord nr 34
rekord nr 35
rekord nr 36
rekord nr 37
14
1
2
3
4
5
6
7
8
9
10
11
12
13
14

Wyjście
rekord nr 37
rekord nr 36
rekord nr 35
1 [2] [3] [4] ... [13]

rekord nr 34
rekord nr 33
rekord nr 32
[1] 2 [3] [4] [5] ... [13]

rekord nr 31
rekord nr 30
rekord nr 29
[1] [2] 3 [4] [5] [6] ... [13]

rekord nr 28
rekord nr 27
rekord nr 26
[1] [2] [3] 4 [5] [6] [7] ... [13]

rekord nr 25
rekord nr 24
rekord nr 23
[1] [2] [3] [4] 5 [6] [7] [8] ... [13]

rekord nr 22
rekord nr 21
rekord nr 20
[1] ... [3] [4] [5] 6 [7] [8] [9] ... [13]

rekord nr 19
rekord nr 18
rekord nr 17
[1] ... [4] [5] [6] 7 [8] [9] [10] ... [13]

rekord nr 16
rekord nr 15
rekord nr 14
[1] ... [5] [6] [7] 8 [9] [10] [11] ... [13]

rekord nr 13
rekord nr 12
rekord nr 11
[1] ... [6] [7] [8] 9 [10] [11] [12] [13]

rekord nr 10
rekord nr 9
rekord nr 8
[1] ... [7] [8] [9] 10 [11] [12] [13]

rekord nr 7
rekord nr 6
rekord nr 5
[1] ... [8] [9] [10] 11 [12] [13]

rekord nr 4
rekord nr 3
rekord nr 2
[1] ... [9] [10] [11] 12 [13]

rekord nr 1
[1] ... [10] [11] [12] 13

HTTP 404

---

Ułamki dziesiętne

 

Dziś› Jasiu poznaje ułamki dziesiętne i ich rodzaje. Pani matematyczka przedstawił‚a właśnie uczniom sposób zamiany uł‚amka zwykłego na dziesiętny: wystarczy podzielić‡ licznik przez mianownik i otrzymujemy uł‚amek w postaci dziesiętnej, czasami okresowy nieskończony. Twoim zadaniem jest przedstawienie ułamka dziesią™tnego w postaci ułamka niewłaściwego. Wynik przedstaw w postaci nieskracalnej.

Wejś›cie

W pierwszym wierszu jedna liczba n określająca ilość liczb do zamiany (n < 1000000).

W kolejnych n wierszach uł‚amki dziesiętne nieokresowe lub okresowe (długość‡ wszystkich znaków przedstawiają…cych uł‚amek jest nie wię™ksza niż 15). Czść cał‚kowita ułamka mieści się™ w przedziale [0..1000]. Dane są… tak dopasowane aby do obliczeń„ wystarczył‚y typy 64 bitowe. W reprezentacji ułamka wykorzystany jest znak przecinka, natomiast część okresowa ułamka zawarta jest w zwykłych nawiasach.

Wyjś›cie

Dla każdego testu ułamek w postaci niewłaściwej nieskracalnej w formie [licznik]/[mianownik].

Przykł‚ad

Wejś›cie:
3
5
0,2
1,(2)

Wyjś›cie:
5/1
1/5
11/9

---

 

Fibonacci

Dzisiaj na lekcji matematyki dzieci dowiedziały się o ciągu Fibonacciego. I tak powstała gra, którą od razu wymyślili Jasiu i Stasiu. Zasady są proste. Stasiu podaje dwa słowa, które są pierwszymi wyrazami ciągu oraz liczbę całkowitą k. Kolejne wyrazy ciągu powstają poprzez konkatenację dwóch poprzednich wyrazów. I tak na przykład dla dwóch pierwszych wyrazów: ot i co dalej otrzymujemy: otco, cootco, otcocootco, itd.. Jasiu musi wyznaczyć k-ty wyraz ciągu, którego dwa pierwsze wyrazy są zdefiniowane przez Stasia. Ponieważ ciąg bardzo szybko rośnie i niektórych wyrazów nie sposób zapisać w rozsądnym czasie, wystarczy, że Jasiu poda ile razy pojawia się każda litera alfabetu w k-tym wyrazie ciągu.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (0 < d < 100) oznaczająca liczbę zestawów danych. W kolejnych wierszach znajdują się zestawy danych. Każdy zestaw składa się z dwóch ciągów złożonych z małych liter alfabetu łacińskiego oraz liczby całkowitej k (1 ≤ k ≤ 50). Długość dwóch ciągów nie przekracza łącznie 30 znaków. 

Wyjście
Dla każdego zestawu należy wypisać ciąg 26-ciu liczb całkowitych, które w kolejności występowania oznaczają liczbę poszczególnych liter (a-z) w k-tym wyrazie ciągu.

Przykład

Wejście
3
fraktal to 3
fajny konkurs 4
ot co 5 

Wyjście
2 0 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 1 0 2 0 0 0 0 0 0
1 0 0 0 0 1 0 0 0 1 4 0 0 3 2 0 0 2 2 0 2 0 0 0 1 0
0 0 3 0 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 2 0 0 0 0 0 0

---

Tajemnicze zadanie

Od jakiegoś czasu Jasiu próbuje rozwiązać arcytrudne zadanie, które znajduje się na polskim spoju. To tajemnicze zadanie potrafi rozwiązać tylko określona grupa ludzi, niestety Jasio do nich się nie zalicza. Z pewnego źródła dowiedział się, że zaszyfrowany poniżej tekst przedstawia klucz do sukcesu. Dodatkowo nasz bohater zdobył częstotliwości występowania liter w oryginalnym tekście co znacznie ułatwia odszyfrowanie tekstu.

Na podstawie podanej częstotliwości występowania liter złam szyfr.

Wejś›cie

W pierwszych 26 wierszach częstotliwości wystę™powania poszczególnych liter w tekś›cie oryginalnym podane z dokładnością… do pię™ciu cyfr po przecinku w formacie -

litera a częstotliwość
litera b częstotliwość
litera c częstotliwość‡ itd.

Nastapnie zaszyfrowany tekst (szyfrogram) składający się z nie więcej niż 1000 wierszy oraz w każdym wierszu znajduje się™ nie więcej niż 1000 znaków.

Częstotliwość‡ podanych liter odnosi się™ jednocześ›nie do małych i dużych odpowiedników.

W zaszyfrowanym tekś›cie pojawią… się™ takźe inne znaki, które nie został‚y zaszyfrowane. 

Częstotliwość każdej litery jest unikatowa.

Wyjście

Na wyjściu powinien pojawić‡ się™ oryginalny tekst. Wielkość liter musi się zgadzać.

Przykład

Wejś›cie:
a 0.11172
b 0.01648
c 0.04579
d 0.04029
e 0.06777
f 0.00183
g 0.02015
h 0.00549
i 0.08242
j 0.01832
k 0.03663
l 0.05678
m 0.02747
n 0.05311
o 0.08059
p 0.03114
q 0.00000
r 0.05495
s 0.03480
t 0.04212
u 0.02198
v 0.00000
w 0.03846
x 0.00000
y 0.04762
z 0.06410
Dlhdlewfhc hl cohomwo Poqf dxlgqfpv Gosyzo - evbyoxacv cqwacoa zlqfaczo :).
Dlelhcfmwo e xlcewocveomwk cohom mo zlmzkxbwf dxlixopwbyvacmvp TXOZYOQ - WWW fhvaso.
Zlmzkxb yfm dxcfcmoaclmv sfby hqo qkhcw, zylxcv coacvmoso dxcvilhf c dxlixopleomwfp,
qkgwo xveoqwcoasf, auao dlhbczlqwa bwf e dxlixopleomwk w evzlxcvbyveomwk oqilxvyple,
qkgwo qopwiqlezw, dxlgqfpv oqilxvypwacmf w auao hlgxcf choa poykxf w mwf yvqzl.
Mwfzylxf cohomwo bo gosfacmwf dxlbyf, wmmf cob evpoioso lh dxlixopwbyv mwfal ewfzbcfil evbwqzk.
Zxlyzl plewoa, zochv cmoshcwf alb hqo bwfgwf. 
Mobyfdksoav awoi qwyfx sfby dl yl, ogv codfemwa kmwzoylelba dleylxcfm homvau qwyfx: QHQQWQQHQQHQQ
Q

Uwaga! Oryginalna wiadomość‡ nie został‚a podana celowo, po odszyfrowaniu pojawi się™ tekst z sensem.

---

Ciąg EKG

Ciąg EKG to ciąg liczb całkowitych dodatnich zdefiniowany następująco: pierwsze dwa wyrazy ciągu to 1, 2, a każdy następny wyraz jest najmniejszą liczbą całkowitą dodatnią, która do tej pory nie wystąpiła w ciągu i która nie jest względnie pierwsza z wyrazem bezpośrednio poprzedzającym. Poniżej kilka początkowych wyrazów ciągu:

        1, 2, 4, 6, 3, 9, 12, 8, 10, 5, 15, 18, 14, 7, 21, 24, 16

Ciąg ten nazywany jest ciągiem EKG, ponieważ jego wykres przypomina elektrokardiogram. Ciąg ten ma tę własność, że wszystkie liczby całkowite dodatnie prędzej czy później pojawią się w nim. Twoim zadaniem jest wyznaczyć pozycję w ciągu dla danej liczby całkowitej.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (1 ≤ d ≤ 1000) oznaczająca liczbę przypadków testowych. Każdy przypadek testowy to jedna liczba całkowita a (1 ≤ a ≤ 3 · 105).

Wyjście
Dla każdej liczby podanej na wejściu należy wyznaczyć jej pozycję porządkową w ciągu EKG.

Przykład

Wejście
5
1
2
3
10
15

Wyjście
1
2
5
9
11

---

Modulo 10

 

Dla zadanej liczby binarnej, okreś›l, czy jest ona podzielna przez 10=(1010)2.

Wejś›cie

W pierwszym wierszu jedna liczba n (n < 10 000) określająca liczbę™ zestawów danych.

Kaźdy zestaw skł‚ada się™ z jednej liczby binarnej złoźonej z nie wię™cej niź 1000 bitów.

Wyjście

Dla każdej liczby wypisz Tak, jeśli zadana liczba dzieli się™ bez reszty przez 10 lub Nie w przeciwnym razie.

Przykł‚ad

Wejś›cie:
3
101
111110100
10111

Wyjście:
Nie
Tak
Nie

---

Podział kuli

Na ile maksymalnie części, niekoniecznie równych, można podzielić kulę za pomocą n płaszczyzn?

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (0 < d < 100) oznaczająca liczbę przypadków testowych. Każdy przypadek to jedna liczba całkowita n (0 < n < 2000000) oznaczająca liczbę płaszczyzn.

Wyjście
Dla każdego przypadku testowego należy udzielić odpowiedzi na pytanie postawione w treści zadania.

Przykład

Wejście
3
1
2
3

Wyjście
2
4
8

---

DOMINO II

 

Dziś są dni otwarte Bajtlandzkiej uczelni. Każdy może zapoznać się z wykładowcami, porozmawiać z nimi na różne tematy i przede wszystkim zmierzyć się z nimi intelektualnie. Profesor Algobit przygotował dla swoich potencjalnych studentów grę domino składającą się z 28 kamieni. Na obydwu końcach każdego klocka znajduje się pewna liczba oczek należąca do zbioru {0, 1, 2, 3, 4, 5, 6} oraz każda kombinacja występuje dokładnie raz. Uczniowie szkół ponadgimnazjalnych chętnie podchodzili do stanowiska profesora będąc przekonani, że za chwilę rozegrają fascynującą grę w domino. Niestety bardzo się mylili. Wykładowca rozdał dwa zestawy po tyle samo kamieni - jeden dla siebie, drugi dla swojego przeciwnika, odkrył wyszystkie kamienie i zadał pytanie: "Jeśli ja zaczynam grę i każdy z nas będzie dokładał kamienie zgodnie z zasadami gry domino w taki sposób, że jeśli po zakończonej grze weźmiemy ze stołu dwa dowolne sąsiadujące ze sobą kamienie, to jeden będzie mój a drugi twój, to ile maksymalnie może znaleźć się kamieni na stole?". Zadanie okazało się twardym orzechem do zgryzienia. Jeśli chcesz podejść do profesora Algobita, to wcześniej napisz program, który rozwiąże tą zagadkę, a wiedz, że wtedy profesor zarekomenduje twoje umiejętności.

Wejś›cie

W pierwszym wierszu liczba n określająca liczbę zestawów danych (n ≤ 103).

Każdy zestaw składa się z jednej liczby n określającej po ile kamieni będzie rozdane dla każdego z przeciwników (n należy do zbioru {1, 2, 3, .., 14}. W następnych dwóch wierszach po dwie porcje po n kamieni domina. Pierwszy zestaw to kamienie prof. Algobita, zaś drugie Twoje.

Każdy kamień jest zapisany w postaci: [liczba oczek]|[liczba oczek] np. 3|0. Liczba oczek to liczba należąca do zbioru {0, 1, 2, 3, 4, 5, 6} oraz kamienie są unikatowe.

Jest tylko kilka przypadków testowych, w których znajduje się maksymalna liczba kamieni.

Wyjś›cie

Dla każdego zestawu jedna liczba określająca maksymalną długość kamieni domina przy optymalnej grze, jeśli wiadomo, że pierszy ruch należy do profesora Algobita.

Przykł‚ad

Wejś›cie:
4
4
1|0 2|1 1|5 2|0 
3|2 3|3 3|0 4|1 
5
6|1 4|6 4|5 6|6 5|3 
4|4 0|1 2|6 0|5 2|4 
3
3|3 0|0 1|2 
4|2 6|1 2|0 
2
3|2 0|6 
2|5 1|6 

Wyjście:
2
4
4
2

---

Metryka miasto

Bitek odpowiedzialny jest za organizację spotkań członków Ochotniczej Straży Binarnej w Bitogrodzie. Za każdym razem kiedy chce zorganizować spotkanie, wysyła do wszystkich członków SMS, a każdy członek zainteresowany spotkaniem odpowiada Bitkowi, wysyłając swoje koordynaty najbliższego skrzyżowania. Ulice w mieście tworzą siatkę, po której można poruszać się w metryce miasto, a punkty kratowe tej siatki są skrzyżowaniami. Na podstawie przesłanych koordynatów, Bitek wybiera na spotkanie takie skrzyżowanie, aby zminimalizować sumę odległości przebytą przez członków OSB. Twoim zadaniem jest wyznaczenie tej sumy.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (0 < d < 100) oznaczająca liczbę zestawów danych. W kolejnych wierszach znajdują się zestawy danych. Pierwszy wiersz każdego zestawu to liczba całkowita n (0 < n < 1000) oznaczająca liczbę zainteresowanych spotkaniem członków OSB. W kolejnychn wierszach podane są po dwie liczby całkowite, x, y (0 ≤ x, y ≤ 106) oznaczające koordynaty skrzyżowań wysłane przez członków OSB.

Wyjście
Dla każdego zestawu należy wyznaczyć sumę odległości przebytą przez członków OSB do wyznaczonego przez Bitka skrzyżowania.

Przykład

Wejście
2
5
0 0
2 0
1 1
0 3
2 3
4
2 2
2 2
5 1
5 2

Wyjście
10
7

 

---

Pole trapezu

 

Planimetria jest ulubionym dział‚em Jasia. Często zarywał nocki, żeby rozwiązać‡ zadanie z tego na pozór łatwego działu. Tym razem problem zadany przez nauczyciela okazał‚ się™ za trudny. Jasiu zaczął‚ podejrzewać‡, że autor zadania podał za mał‚o danych. Podał on długości dwóch podstaw oraz wpisał w niego okrąg. Na tablicy narysował poniższy rysunek, który być może jest nie do końca dokładny. Jasiu sprawdził, jaka powinna być odpowiedź i wszystko mu się wyjaśniło. Twoim zadaniem jest wyznaczenie pola tego trapezu mając podane długości podstaw oraz wskazówki z treści zadania.

Wejś›cie

Wejście skł‚ada się™ z pewnej liczby zestawów danych. Kaźdy zestaw skł‚ada się z dwóch liczb cał‚kowitych określających dł‚ugoś›ci podstaw trapezu (a, b < 216).

Wyjście

Dla kaźdego zestawu danych pole szukanego trapezu. Wynik przedstaw z dokładnością… do dwóch miejsc po przecinku.

Przykł‚ad

Wejście:
2
2 8
8 2

Wyjście:
20.00
20.00

 

---

Ciąg cyfr

W podanym ciągu cyfr, wstaw między cyfry przecinki tak, aby utworzyć ciąg ściśle rosnący liczb całkowitych dodatnich o możliwie najmniejszej wartości ostatniego wyrazu.

Wejście
W pierwszym wierszu wejścia znajduje się liczba całkowita d (0 < d < 1000) oznaczająca liczbę przypadków testowych. Każdy przypadek to ciąg cyfr [0-9], którego długość nie przekracza 100. Nie ma ciągu złożonego z samych zer.

Wyjście
Dla każdego przypadku testowego należy podać ciąg liczb oddzielony przecinkami, spełniający warunek ściśle rosnącego, którego ostatni wyraz będzie możliwie najmniejszy.
W przypadku, gdy istnieje więcej niż jeden taki ciąg, należy wypisać ten, którego wyrazy w kolejności występowania mają możliwie największą wartość. Dopuszczamy ponadto zapisywanie zer wiodących na początku liczb. 

Przykład

Wejście
10
234
2635
4638
001
1000101
11091
21000858869201999960
12345678910112
110000011
89217643514707329101953937146641113

Wyjście
2,3,4
26,35
4,6,38
001
100,0101
11,091
21000,85886,92019,99960
12,34,56,78,91,0112
1,10,000011
8921,76435,147073,291019,5393714,6641113

---

Zadanie Maćka

Małego Bajtosława od kilku dni zastanawia problem trójek pitagorejskich. Znając długość jednej z przyprostokątnych rowną 3 znalazł tylko jeden taki trójkąt o bokach 3, 4, 5. Jednak Bajtosława to nie satysfakcjonuje. Znając jedną z przyprostokątnych chciałby wiedzieć, ile takich trójek może znaleźć.

 

Wejście

Na wejsciu podana jest jedna liczba t określająca liczbę zestawów danych (t<100000)

Każdy zestaw danych składa się z jednej liczby a (a<100000),będącej jedną z przyprostokątnych trójkąta prostokątnego.

Wyjście

Dla każdego zestawu danych jedna liczba będąca szukaną przez Bajtosława.

Przykład

Wejście:
3
3
8
11

Wyjście:
1
2
1

---

Bitcoin

 Profesor Algobit jest twórcą… nowego projektu uczelnianego polegającego na produkcji wirtualnych monet Bitcoin'ów w celu zasilenia opł‚akanego budżetu uczelni. Do współpracy zaprosił‚ najlepszych pię™ciu programistów, między innymi Ciebie. Warunkiem koniecznym do wzię™cia udział‚u w projekcie jest posiadanie komputera osobistego, który bę™dzie wykonywał zlecenia skomplikowanych obliczeń, za co szkoła otrzyma wynagrodzenie w postaci bitmonet. Dodatkowo profesor otrzymał‚ pewien budżet, dzięki któremu bę™dzie można rozbudować‡ komputery programistów w celu zwię™kszenia mocy obliczeniowej komputerów i przyspieszeniu generowania profitów. Niestety pienię™dzy tych nie można podzielić‡ po równo mię™dzy programistów, ponieważ niektóre komputery lepiej reagują na rozbudowę™ i nawet niewielki wkł‚ad finansowy znacznie korzystniej wpływa na generowanie Bitcoin'ów niż inne. 

Znają…c wpł‚yw rozbudowy komputera na generowanie wirtualnych monet każdego programisty, określ ile maksymalnie można zwię™kszyć‡ produkcję Bitcoin'ów w cią…gu jednej doby mając do dyspozycji n tysięcy zł‚otych.

Wejś›cie

W pierwszym wierszu jedna liczba określająca liczbę zestawów danych (nie więcej niż 1000). 

W pierwszym wierszu każdego zestawu jedna liczba cał‚kowita  n określająca wielkość‡ budżetu (n ∈ [1..1000]).

Nastę™pnie pięć‡ wierszy, w każdym wierszu po n liczb cał‚kowitych (wartości te nie przekraczają 107 oraz reprezentują ciąg niemalejący).

Jeś›li i-ta… liczba… danego wiersza ma wartość k, oznacza to, źe inwestują…c i tysięcy w komuter kolejnego programisty zwię™kszymy dobowo zysk o k Bitcoin'ów.

Wyjś›cie

Dla każdego zestawu jedna liczba określająca maksymalny zysk, jaki można otrzymać‡ inwestują…c n tysię™cy w komputery programistów.

Przykł‚ad

Wejście:
1
4
1 3 3 4
2 4 4 5
1 3 5 5
2 3 3 5
3 3 3 5

Wyjś›cie:
9

Wyjaś›nienie

Inwestują…c 2 tysią…ce w drugi komputer zwię™kszamy jego wydajność o 4, 

inwestują…c w komputer 4 i 5 zwię™kszamy wydajność odpowiednio o 2 i 3. 

W sumie: 4 + 2 + 3 = 9

---

Pięć kół i kwadrat

Profesor Algobit, znany wśród studentów jako srogi i wymagający wykładowca, jako pracę zaliczeniową dla swoich studentów dał z pozoru bardzo trudne zadanie. Narysował kwadrat oraz pięć losowych okręgów. Podał niezbędne współrzędne tych figur i nakazał zamalować część wspólną tych okręgów z kwadratem, a następnie poprosił, aby policzyli oni jaki procent kwadratu został zamalowany. Zmartwieni studenci rozeszli się do domów nie mając kompletnie żadnego pomysłu na rozwiązanie tego zadania. Ostatnia nadzieja tkwi w Tobie. Pomóż biednym studentom i napisz program, który wyznaczy, jaki procent danego kwadratu został zamalowany.

Wejście

W pierwszym wierszu jedna niewielka liczba określająca ilość zestawów danych.

Specyfikacja każdego zestawu:

W pierwszym wierszu trzy liczby rzeczywiste: współrzędne xk, yk oraz n określające odpowiednio współrzędne górnego lewego rogu kwadratu oraz długość boku (|xk| < 100, |yk| < 100 oraz n  nie większe niż 100.

Następnie pięć wierszy. W każdym z tych wierszy po trzy liczby x, y oraz r, określające współrzędne środka okręgu oraz jego promień.

Wszystkie wartości na wejściu są podane z dokładnością do dwóch miejsc po przecinku. 

Wyjście

Dla każdego zestawu testowego jedna liczba zaokrąglona do pełnych procentów. Bezpośrednio po tej liczbie wypisujemy znak '%'.

Przykład 1

Wejście:
1
0.00 0.00 5.00
0.00 0.00 2.00
5.00 0.00 2.00
0.00 -5.00 2.00
5.00 -5.00 2.00
7.00 0.00 2.00

Wyjście:
50%

Przykład 2

Wejście:
1
0.00 2.00 2.00
1.00 1.00 1.00
1.00 1.00 0.50
1.00 1.00 0.25
2.00 2.00 1.00
2.00 0.00 1.00

Wyjście:
89%

Poniższy rysunek przezentuje drugi przyład:

---

T9

Napisz program, który sprawdzi, czy podane słowo mogło powstać z danej kombinacji cyfr dzięki słownikowi T9.

 

 

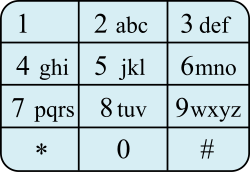
Input

W pierwszym wierszu jedna liczba t (0<t<100) oznaczająca liczbę zestawów testowych.

W kolejnych wierszach po dwa wyrazy, złożone z dużych i małych liter liter alfabetu angielskiego, oraz cyfr 0-9*. Długość wyrazów jest zawsze taka sama inie przekracza 200.

 

*a-z, A-Z, 0-9

 

Output

Jeśli z podanej kombinacji liczb można utworzyć dany wyraz, wypisz ‘’TAK - <wyraz>’’ – przykładowo ‘’TAK – Fraktal’’.

Jeśli nie można, wypisz ‘’NIE’’.

Każdy zestaw oddzielany jest znakiem nowej linii.

 

Example

Input:

3

FraKtal 3725825

BlednaKomBinacjA123 2533625662462252122

NIE 643

Output:

TAK – FraKtal

NIE

TAK - NIE

---